In the excerpt of his will in 1895, Alfred Nobel enacted the entirety of his estate to be wielded to bestow
“Prizes to those who, during the preceding year, have conferred the greatest benefit to humankind.”
The 2021 physics prize is awarded in two parts. Part-1 goes jointly to Prof. Syukuro Manabe and Prof. Klaus Hassellmann for the physical modeling of Earth s climate, quantifying variability and reliably predicting global warming”. Part-2 goes to Prof. Giorgio Parisi for his revolutionary contributions to disordered and random phenomena which provides us with a theoretical background for such systems, consequently uplifting our understanding of the said systems.
Our world is full of complex and disordered phenomena and processes. One such system is the interlaced weather and climate. Climate models are designed to understand and predict such complex systems. The climate models help us understand, describe, and then replicate the earth’s climate to give precise estimates on how it will evolve due to natural variations, anthropogenic activity, or a blend of both. The climate models propel humans towards revolutionary policymaking of national, regional, and local importance, based on solid science, which has profound implications. It will better equip us to avoid jeopardising our resources, which are already in deficit.
The work has helped scientists answer the fundamental questions surrounding the debate of climate change:
- Is Earth heating up? Yes.
- Is it the cause of the increased amounts of greenhouse gases in the atmosphere? Yes.
- Can this be explained solely by natural factors? No.
- Are anthropogenic emissions the reason for the increasing temperature? Yes.
We have been provided with a solid physical foundation for our knowledge of Earth s climate. We can no longer say that we did not know – the climate models are unequivocal.
Part-1
In 1960, Prof. Manabe led the development of physical models of the earth’s climate and was the first to explore the interaction between radiation balance and the vertical transport of air masses. Manabe and Wetherald made prudent assumptions to model the climate. Firstly, they assumed the entire atmosphere to be a 1-dimensional column. Secondly, the inclusion of greenhouse gases was more sophisticated, precisely due to the presence of better spectroscopic data. Thirdly, convection was incorporated into the model to represent the upward movement of hot air and the downward movement of cold air in the 1-D model. Finally, the absolute humidity was replaced with relative humidity as it helped include the effect of water vapour feedback, Figure 1 (a).

Manabe’s model corroborated that the heating of earth was due to rising CO2 concentration and not solar irradiation, which was one of the reasons ascribed to the heating. If solar radiations were responsible, the entire atmosphere should have been heating, but on doubling the CO2 concentration, the temperature on the ground increased by 2.36oC, whereas the temperature at about 40 km reduced, Figure 1 (b).
Since there is a lot of talk about models, let’s talk about models for a moment. Models are generally two kinds: Stochastic, Figure 2 (a) and Deterministic, Figure 2 (b). If you run a deterministic model of a system with set initial values for n times, the model will retrace the same path. But if you run a stochastic model n times, it will follow a unique route every single time. There’s a catch. If you run the stochastic model enough times, a specific resultant deterministic path is shown in green in Figure 2 (c).
Let us take an analogy to understand Prof. Klaus Hasselmann’s work. Suppose X takes his dog for a walk in snow, and the tracks of the dog (in red) and X (in green) are shown in Figure 2 (d). By closely observing the dog tracks, the path followed by X can be inferred. It can be concluded whether, at a point, X was in motion or stationary. Here, the dog’s path is analogous to the rapidly changing weather (the stochastic part), and X represents the slowly changing climate (the resultant deterministic path). The decisive trick incorporated by Prof. Klaus Hasselmann was to consider the rapid changes in weather as noise into the calculations and demonstrate how this noise (weather or the stochastic path) affects the climate, the signal (deterministic path).
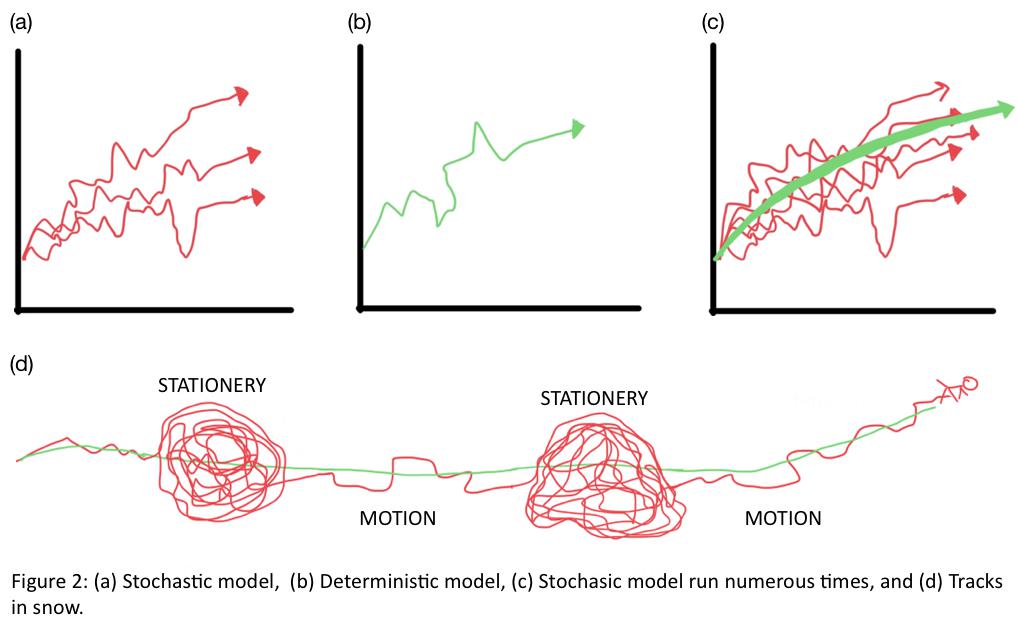
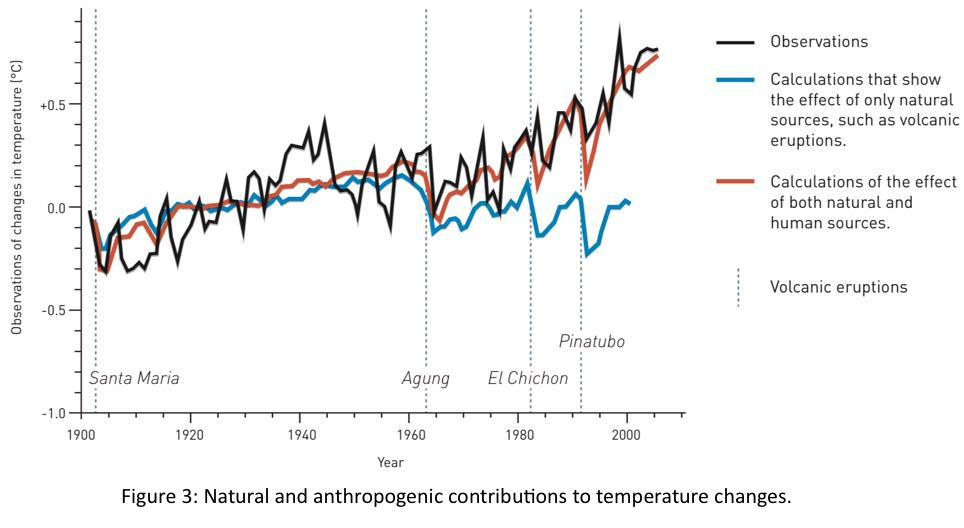
Herein comes another benefit of choosing a stochastic model over a deterministic. If we care about the random occurrences (weather) in your system (climate), the stochastic model will better represent the modelled system. Coupled land, ocean, cryosphere, and anthropogenic emissions lead to rapidly varying weather, affecting the slowly evolving climate. Prof. Hasselmann linked the models with actually recorded climate observations and theoretical considerations to further assign the impact of anthropogenic emissions. He separated the effect of the factors like land, ocean, cryosphere, and anthropogenic emissions and identified them individually. Consider that X takes four dogs (embodying land, ocean, cryosphere, and anthropogenic emissions) on a stroll. By close and peculiar observation of the tracks of the dogs, you can work out the effect of motion of each dog on the movement of X (the climate). This premise helped Hasselmann to prove that the increase in temperature is not solely due to the natural phenomenon and that anthropogenic phenomenon affects it, as shown in Figure 3.
Hasselman’s work will keep improving, particularly because of its inherent property that links the gathered observational data with the climate models and theoretical considerations. As we go further into future, the accuracy of these factors (observational data, climate models and theoretical framework) will improve, leading to better estimates of weather and climate for provident and productive public policymaking.
Part-2
Imagine an equilibrium system just slightly out of the equilibrium. Now consider this system is unable to reach equilibrium due to high free energy barriers. Such a system is a typical example of spin glass, a disordered system, which Prof. Giorgio Parisi extensively studied. The only way such a system (in this case, the climate) will gradually reach equilibrium is by hopping from one metastable state to another. It is possible for such a system to perpetually remain out of equilibrium if it continually agitated with a slowly varying external field (in this case, the weather).
In 1979, Parisi ingeniously used the replica trick to solve the spin-glass problem, a disordered system.
He realised a concealed structure in the replicas and found a way to illustrate them mathematically. This description is crucial in understanding of complex systems, be it neural networks, machine learning, or in the 2021 Nobel Prize in Physics’ case, the climate. The importance of Prof. Parisi’s method in understanding of such frustrated complex systems with the help of a mathematical framework can be understood by a simple analogy. Look at how helpful recognising the underlying mathematics of the first-order processes of nature is. The mathematical background facilitates identifying any first-order process in nature (for example, radioactive methods). The mathematical knowledge allows us to model a first order process and execute them accordingly. Thus, comprehending the mathematical knowledge of any natural phenomenon has profound implications.
Remembering the giants
Fourier s attempt to understand the energy budget of the Earth, Svante Arrhenius’ contribution in developing
early climate models, John Tyndall’s ingenious work in compiling spectroscopic data of gases and many more contributed incredibly to the evolution of climate models to the state at which they are today. Robert Brown’s observation of the pollen grains under the microscope and Einsteins’s attempt to give an analytical solution to Boltzmann’s statistical depiction of the thermodynamical laws and many other moving parts in this incredible machinery of science ultimately led to Giorgio Parisi’s ingenuous solution of complex disordered systems.
As crucial as it is to recognise the ingenuity of the winners of the Physics Nobel Prize, 2021, of similar primacy, is recalling the subtle yet significant work of these giants. As very rightly stated by Isaac Newton in a letter to Robert Hooke, “If I have seen further, it is by standing on the shoulders of Giants.”
Rohit Thakur
Junior Research Fellow
Group of Dr H S S Ramakrishna Matte
CeNS, Bengaluru
